Structure and types
We now describe the way the Quijote simulations are organized and the different cosmological models present on it.
Classes and types
The Quijote simulations can be classified into three broad classes:
Fiducial simulations. Those are simulations with a fiducial cosmology consistent with Planck. They only vary the initial random seed.
Individual parameter variations. Those are simulations where the value of a single parameter is varied with respect to the fiducial simulations. The initial random seed of those simulations are taken to match those of the fiducial model. Those are designed for Fisher matrix calculations.
Multiple parameter variations. Those are simulations that vary simultaneously the value of several parameters and the initial random seed. Those simulations are designed for machine learning applications.
The Quijote simulations can also be classified into different types:
LCDM. Standard simulations with different values of \(\Omega_{\rm m}\), \(\Omega_{\rm b}\), \(h\), \(n_s\), \(\sigma_8\). See LCDM for more details.
Dark Energy. These are simulations were we vary the expansion rate of the Universe through the \(w\) parameter. See Dark energy for more details.
Massive neutrinos. These are simulations that include massive neutrinos as additional particles. See Massive neutrinos for more details.
Separate Universe. These simulations incorporate and overall over(under)density or an amplitude of the DC mode different to zero. See Separate Universe for more details.
Primordial non-Gaussianities. These simulations include primordial non-Gaussianities of different types. See Primordial non-Gaussianities for more details.
Parity violating. These simulations include parity violating features. See Parity-violation for more details.
Modified gravity. These simulations are run with a modified gravity model: \(f(R)\). See Modified Gravity for more details.
Note that these types are not exclusive, i.e. there are simulations that vary LCDM parameters plus the dark energy parameter plus the neutrino masses. The scheme bell shows the different classes of simulations in Quijote:
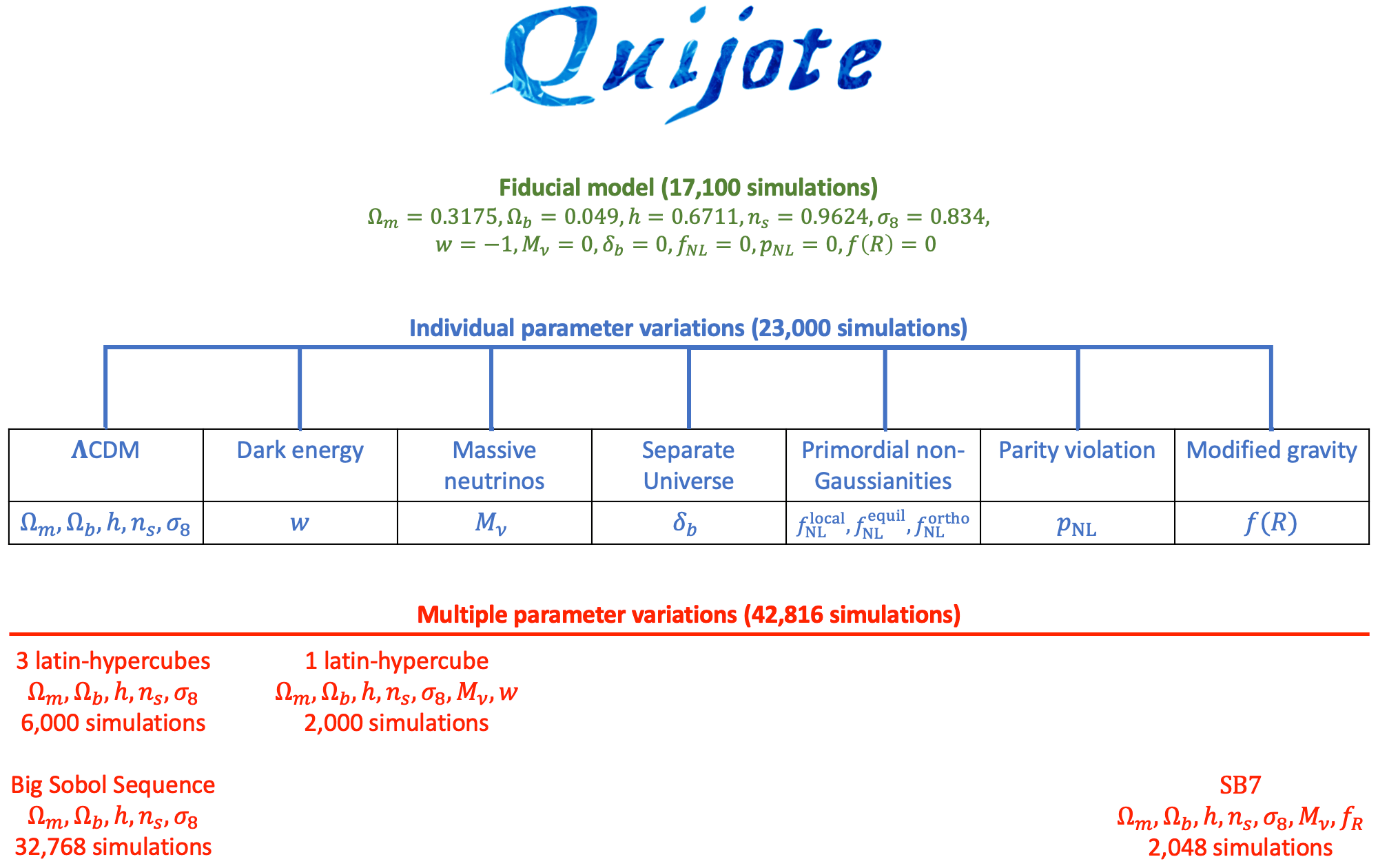
A brief description of the different cosmologies is provided in the below table. The standard and paired fixed snapshots or data products will be located inside the same folder. The paired fixed (or fixed) will be located inside folders starting with NCV (from No Cosmic Variance). Further details can be found in the Quijote paper and Quijote-PNG paper.
Name |
\(\Omega_m\) |
\(\Omega_b\) |
\(h\) |
\(n_s\) |
\(\sigma_8\) |
\(M_\nu\) |
\(w\) |
\(\delta_b\) |
\(f_{\rm NL}^{\rm loc}\) |
\(f_{\rm NL}^{\rm equ}\) |
\(f_{\rm NL}^{\rm ort1}\) |
\(f_{\rm NL}^{\rm ort2}\) |
\(p_{\rm NL}\) |
\(f_{R_0}\) |
realizations |
simulations |
ICs |
\(N_c^{1/3}\) |
\(N_\nu^{1/3}\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
fiducial |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
15,000 |
standard |
2LPT |
512 |
0 |
fiducial |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
fiducial_ZA |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
Zeldovich |
512 |
0 |
fiducial_LR |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1,000 |
standard |
2LPT |
512 |
0 |
fiducial_HR |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
100 |
standard |
2LPT |
1,024 |
0 |
Om_p |
0.3275 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
Om_p |
0.3275 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
Om_m |
0.3075 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
Om_m |
0.3075 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
Ob2_p |
0.3175 |
0.051 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
Ob2_p |
0.3175 |
0.051 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
Ob2_m |
0.3175 |
0.047 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
Ob2_m |
0.3175 |
0.047 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
Ob_p |
0.3175 |
0.050 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
Ob_m |
0.3175 |
0.048 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
h_p |
0.3175 |
0.049 |
0.6911 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
h_p |
0.3175 |
0.049 |
0.6911 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
h_m |
0.3175 |
0.049 |
0.6511 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
h_m |
0.3175 |
0.049 |
0.6511 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
ns_p |
0.3175 |
0.049 |
0.6711 |
0.9824 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
ns_p |
0.3175 |
0.049 |
0.6711 |
0.9824 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
ns_m |
0.3175 |
0.049 |
0.6711 |
0.9424 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
ns_m |
0.3175 |
0.049 |
0.6711 |
0.9424 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
s8_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.849 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
s8_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.849 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
s8_m |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.819 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
s8_m |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.819 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
2LPT |
512 |
0 |
Mnu_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0.1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
Zeldovich |
512 |
512 |
Mnu_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0.1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
Zeldovich |
512 |
512 |
Mnu_pp |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0.2 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
Zeldovich |
512 |
512 |
Mnu_pp |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0.2 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
Zeldovich |
512 |
512 |
Mnu_ppp |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0.4 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
Zeldovich |
512 |
512 |
Mnu_ppp |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0.4 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
paired fixed |
Zeldovich |
512 |
512 |
w_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1.05 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
Zeldovich |
512 |
0 |
w_m |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-0.95 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
Zeldovich |
512 |
0 |
DC_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
+0.035 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
Zeldovich |
512 |
0 |
DC_m |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
-0.035 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
Zeldovich |
512 |
0 |
LC_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
+100 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
LC_m |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
-100 |
0 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
EQ_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
+100 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
EQ_m |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
-100 |
0 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
OR_CMB_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
+100 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
OR_CMB_m |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
-100 |
0 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
OR_LSS_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
+100 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
OR_LSS_m |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
-100 |
0 |
0 |
500 |
standard |
2LPT |
512 |
0 |
ODD_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
+1e6 |
0 |
500 |
standard |
2LPT |
512 |
0 |
ODD_m |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
-1e6 |
0 |
500 |
standard |
2LPT |
512 |
0 |
fR_p |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
-5e-7 |
500 |
standard |
Zeldovich |
512 |
0 |
fR_pp |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
-5e-6 |
500 |
standard |
Zeldovich |
512 |
0 |
fR_ppp |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
-5e-5 |
500 |
standard |
Zeldovich |
512 |
0 |
fR_pppp |
0.3175 |
0.049 |
0.6711 |
0.9624 |
0.834 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
-5e-4 |
500 |
standard |
Zeldovich |
512 |
0 |
latin_hypercube |
[0.1 - 0.5] |
[0.03 - 0.07] |
[0.5 - 0.9] |
[0.8 - 1.2] |
[0.6 - 1.0] |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2,000 |
standard |
2LPT |
512 |
0 |
latin_hypercube |
[0.1 - 0.5] |
[0.03 - 0.07] |
[0.5 - 0.9] |
[0.8 - 1.2] |
[0.6 - 1.0] |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2,000 |
standard |
2LPT |
512 |
0 |
latin_hypercube |
[0.1 - 0.5] |
[0.03 - 0.07] |
[0.5 - 0.9] |
[0.8 - 1.2] |
[0.6 - 1.0] |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2,000 |
standard |
2LPT |
1,024 |
0 |
nwLH |
[0.1 - 0.5] |
[0.03 - 0.07] |
[0.5 - 0.9] |
[0.8 - 1.2] |
[0.6 - 1.0] |
[0.01 - 1.0] |
[-1.3 - -0.7] |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2,000 |
standard |
Zeldovich |
512 |
512 |
SB7 |
[0.1 - 0.5] |
[0.03 - 0.07] |
[0.5 - 0.9] |
[0.8 - 1.2] |
[0.6 - 1.0] |
[0.01 - 1.0] |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
[ -3e-4 - 0] |
2,048 |
standard |
Zeldovich |
512 |
512 |
BSQ |
[0.1 - 0.5] |
[0.02 - 0.08] |
[0.5 - 0.9] |
[0.8 - 1.2] |
[0.6 - 1.0] |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
32,768 |
standard |
2LPT |
512 |
0 |
Simulations with \(\delta_b \neq 0\) correspond to separate universe simulations and therefore have an amplitude of the DC mode different than 0 (or equivalently, a curvature different than 0). See Separate Universe for further details on these simulatons.
Simulations with \(f_{\rm NL} \neq 0\) correspond to simulations with primordial non-Gaussianities (Quijote-PNG). See Primordial non-Gaussianities for further details on these simulations.
Simulations with \(p_{\rm NL} \neq 0\) correspond to simulations with parity-violating initial conditions (Qujjote-ODD). See Parity-violation for further details on these simulations.
Simulations with \(f_{R_0} \neq 0\) correspond to simulations with modified gravity (Quijote-MG). See Modified Gravity for further details on these simulations.
Simulations with parameters in brackets correspond to the latin-hypercubes and sobol sequences simulations. See Latin-hypercubes and Big Sobol Sequence for further details on these simulations.